Quadratische Gleichungen .

Quadratische Gleichungen sind Gleichungen der Form

d = ax² + bx + c .

Sie lassen sich durch relativ einfache Umformungen auf die Schreibform

0= x² + px + q

bringen. Es kann für die Gleichung keine, eine oder zwei Lösungen geben.

Neben der p-q-Formel gibt es noch die Möglichkeit
- die Lösungen zu raten (vornehmer: durch Anwendung des Satzes von Vieta)
- oder im Falle, dass q = 0 ist (also garnicht erst auftritt), das x auszuklammern und dadurch den Term zu faktorisieren.

Für quadratische Gleichungen der Form

0= x² + px + q

gibt es die p-q-Formel (Herleitung) als Lösungsformel. Sie lautet:

x₁ = ^-p/₂ - wurzel( (^p/₂)² - q) bzw.
x₂ = ^-p/₂ + wurzel( (^p/₂)² - q)

Der folgende Gleichungslöser verwendet diese p-q-Formel. Geben Sie die konkreten Werte für p und q ein, clicken Sie "Rechne!" an, und Sie erhalten die Lösung, gleichzeitig wird Ihr Konto mit 1,30 Euro pro Rechenvorgang belastet......

Beispiel: Bei der Gleichung 0 = x² - 6x - 4 geben Sie als p die ´-6´ und als q die ´-4´ ein.

Seitenanfang

Satz von Vieta

Multipliziert man spasseshalber einige Produkte der Form (x + a)(x + b) aus, so stellt man bald eine Gesetzmässigkeit fest - das hat auch Herr Vieta, franz. Mathematiker (1540 - 1603) und der hat sie aufgeschrieben, die Gesetzmässigkeit. Hier wird sie an nur Zahlenbeispielen verdeutlicht:

(x - 5)(x + 2) = x² + 2x - 5x -10 = x²- 3x -10 -> -5 * 2 = -10 und -5 + 2 = -3

oder
(x + 7)(x - 1) = x² - 1x + 7x - 7 = x² + 6x - 7 -> 7 *(-1) = -7 und 7 + (-1) = 6

oder
(x + 2)(x + 9) = x² + 9x + 2x + 18 = x² + 11x + 18 -> 2 * 9 = 18 und 2 + 9 = 11

und nun abstrakter:
(x + a)(x + b) = x² + bx + ax + ab = x²+ (a + b)x + ab

-> Und jetzt zur Anwendung:
Sucht man die Lösungen zur Gleichung   0 = x² + x - 6 , so kann man versuchen, den rechten Teil der Gleichung in ein Produkt umzuformen; dies geht recht oft gut, wenn man die obigen Beispiele rückwärts liest. In diesem Fall kann die Zahl ´-6´ entstanden sein als das Produkt der Zahlen ´2´ und ´-3´ oder auch von ´-2´ und ´3´ oder auch...   Nun muss aber auch die Summe der beiden Werte passen: es muss erste Zahl plus zweite Zahl den Wert vor dem ´x´ ergeben! Hier passt die Kombination ´-2´ und ´3´,
denn 1).   -2 * 3 = -6
und   2).   -2 + 3 = +1

Also kann man schreiben:

0 = x² + x - 6    anders:
0 = (x - 2) * (x + 3)   und damit:
         x₁= 2   x₂ = -3

Nochmal:
0 = x² - x - 20    anders:
0 = (x - 5) * (x + 4)   und damit:
         x₁= 5   x₂ = -4

Aller guten Dingen sind dreiquadrat:
0 = x² + 4x - 12    anders:
0 = (x - 2) * (x + 6)   und damit:
         x₁= 2   x₂ = -6

Der Satz von Vieta ist nur dann effektiv angewendet, wenn man nach sehr kurzer Zeit durch Intuition und Glück die Zerlegung gefunden hat. Muss man anfangen zu Rechnen (etwa mit einem Gleichungssystem), so findet man die Lösung sicher mit der p-q-Formel schneller!

´Raten´ Sie mal die passenden Werte für 0 = x² - ²/₇x + ⁸/₁₅ !
Nee, lassen Sie mal lieber, Ihr Partner wollte dieses Wochenende doch was mit Ihnen unternehmen, oder?

Seitenanfang

Im Spezialfall, dass q = 0 ist, mit anderen Worten:

0= x² + px

kann man eine Faktorisierung durch ausklammern von ´x´ erreichen; damit hat man gewonnen, wie das folgende Beispiel zeigt:

0= x² + 9x

wird zu:

0= (x + 9) * x

und hat die Lösungen:

x₁ = -9 und x₂ = 0

Seitenanfang

Herleitung der p-q-Formel durch quadratische Ergänzung

Zahlenbeispiel	allgemeine Rechnung	Bemerkungen
0 = x² - 6x - 4	0 = x² + px + q	zurückführen auf Scheitelpunktform
0 = x² - 6x + (9 - 9)- 4	0 = x² + px + ((p/2)² - (p/2)²) + q	passende Ergänzung ´reinmogeln´ (in der Klammer steht jeweils 0 !
0 = (x² - 6x + 9) - 9- 4	0 = (x² + px + (p/2)² ) - (p/2)² + q	Umdenken; durch Klammerung sichtbar machen
0 = (x - 3)² - 9- 4	0 = (x + (p/2))²- (p/2)² + q	binomische Formel anwenden (und ggf. zusammenrechnen)
0 = (x - 3)² - 13	(hier geschieht gerade nichts)	sortieren, um an das ´x´ zu kommen
13 = (x - 3)²	(p/2)² - q = (x + (p/2))²	Wurzel ziehen (daran denken, dass zwei Lösungen vorhanden sind)
+wurzel(13) = x - 3 oder -wurzel(13) = x - 3	+wurzel((p/2)² - q) = x + (p/2) oder -wurzel((p/2)² - q) = x + (p/2)	nach ´x´ auflösen
3 + wurzel(13) = x₁ oder 3 - wurzel(13) = x₂	-(p/2) + wurzel((p/2)² - q) = x₁ oder -(p/2) - wurzel((p/2)² - q) = x₂	hier sind die beiden Lösungen!

Quadratische Ergänzung

In Basis Mathematik 9 findet sich folgende Erklärung: ``Quadratische Ergänzung'' bedeutet, dass man ein vollständiges Quadrat der Form $x^{2}+2ax+a^{2}=\left( x+a\right) ^{2}$ durch geeignete Ergänzung herstellen muss. Damit eine Äquivalenzumformung gewährleistet ist, muss auf beiden Seiten der Gleichung dieselbe Ergänzung durchgeführt werden!

Herleitung der Lösungsformel mittels quadratischer Ergänzung:
Durch Division durch $a$ erhält man die Normalform $x^{2}+\frac{b}{a}x+\frac{c}{a}=0$ , diese wird mit $\left( \frac{b}{2a}\right) ^{2}$ ergänzt. Damit folgt: $x^{2}+\frac{b}{a}+\left( \frac{b}{2a}\right) ^{2}-\left( \frac{b}{2a}\right) ^{2}+\frac{c}{a}=0$ , $\left( x+\frac{b}{2a}\right) ^{2}-\frac{b^{2}}{4a^{2}}+\frac{c}{a}=0$ und so $\left( x+\frac{b}{2a}\right) ^{2}-\frac{b^{2}-4ac}{4a^{2}}=0$ . Schreibt man den Minuenden als Quadrat und formt mittels dritter binomischer Formel um, so erhält man: $\left( \left( x+\frac{b}{2a}\right) +\frac{\sqrt{b^{2}-4ac}}{2a}\right) \left( \left( x+\frac{b}{2a}\right) -\frac{\sqrt{b^{2}-4ac}}{2a}\right) =0$ und damit die oben angegebenen Lösungen. Die quadratische Ergänzung macht dem Schüler meist Probleme, da immer mit dem Betrag gerechnet wird.

Zur Verdeutlichung ein Beispiel:

$4x^{2}+11x-3=0$		Division durch 4
$x^{2}+\frac{11}{4}x-\frac{3}{4}=0$		Normalform
$x^{2}+\frac{11}{4}x=\frac{3}{4}$		"Sortieren"
$x^{2}+2x\cdot \frac{11}{8}+\left( \frac{11}{8}\right) ^{2}$ = $\frac{3}{4}+\left( \frac{11}{8}\right) ^{2}$		quadratische Ergänzung
$\left( x+\frac{11}{8}\right) ^{2}=\frac{3}{4}+\frac{121}{64}$ = $\frac{169}{64}$
$\left\vert x+\frac{11}{8}\right\vert =\frac{13}{8}$		Betragsstriche!

Damit ergeben sich als Lösungen: $x+\frac{11}{8}=\frac{13}{8}\Rightarrow x=\frac{1}{4}$ und $x+\frac{11}{8}=-\frac{13}{8}\Rightarrow x=-3$ . Da es sich hier um Äquivalenzumformungen handelt ist keine Probe notwendig.

Charakteristische Fehlerquellen sind:

Die Division durch den Koeffizienten des quadratischen Terms darf nicht vergessen werden
Bei der Ergänzung muss das Quadrat des halben Koeffizienten des linearen Terms - und zwar auf beiden Seiten! - ergänzt werden.
Um die Lösung mit den Betrag richtig interpretieren zu können, ist eine verständliche Einführung des Betrags notwendig, da sonst nicht alle Lösungen gefunden werden.

Nach einer Übungsphase der verschiedenen Lösungsmethoden schließen sich folgende Aufgabenstellungen an: Wie viele Lösungen besitzt die Gleichung $2y^{2}=\frac{1}{5}y+\frac{3}{5}$ ?
bzw.
Bestimme die Anzahl der Lösungen in Abhängigkeit vom Parameter k: $0,25kx^{2}-\left( k-1\right) x+k=0$ .

AL-CHARIZMI (lebte um 800) zeigt seinen Lesern einen geometrischen Beweis der quadratischen Ergänzung (hier am Beispiel $x^{2}+10x-56=0$ ):
Ausgegangen wird vom Quadrat ABCD, dessen Flächeninhalt genau dem gesuchten $x^{2}$ entspricht. Danach soll eine Fläche vom Inhalt 10mal der gesuchten Zahl, also $10x$ , hinzugefügt werden. Zu diesem Zweck wird die 10 halbiert und die Fläche $5x$ rechts und unten an das Quadrat gezeichnet. Somit weis man, dass das große Quadrat mit den zwei hinzugefügten Rechtecken die Fläche 56 ausmacht. Das kleine Quadrat mit Inhalt 25 ist also noch zuviel, deshalb wird es zu den 56 hinzuaddiert. Als Formel ergibt sich: $\left( x+5\right) ^{2}=81$ und daraus $x=4$ ( $x=-14$ scheidet wegen der geometrischen Betrachtung aus). Dies entspricht genau der gesuchten Quadratseite.

$\resizebox* {0.6\textwidth}{!}{\includegraphics{alcharizmi.eps}}$

Den Abschluss bilden Textaufgaben: z.B.
Herr Hausner kauft bei einem Sonderangebot günstig $22,50m^{2}$ Teppichboden mit $19m$ Wandleiste. Welche Maße hat ein Zimmer mit rechteckiger Grundfläche, wenn der Teppichboden mit der Wandleiste für dieses Zimmer gerade ausreicht (dass man an der Türe keine Stoßleiste benötigt, soll nicht berücksichtigt werden) ? Hier wird neben der quadratischen Gleichung auch noch das Lösen von einfachen Gleichungssystemen wiederholt:
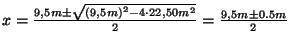Die Seiten des Zimmers seien x und y. Damit ergibt sich: $x\cdot y=22,50m^{2}$ und $2\cdot \left( x+y\right) =19m$ . Aus der zweiten Gleichung erhält man durch Umformung $y=9,5m-x$ und somit $x\cdot \left( 9,5m-x\right) =22,50m^{2}$ , also $9,5m\cdot x-x^{2}=22,50m^{2}\Rightarrow x^{2}-9,5m\cdot x+22,50m^{2}=0$ . Für die Länge x ergibt sich dann: $x=\frac{9,5m\pm \sqrt{\left( 9,5m\right) ^{2}-4\cdot 22,50m^{2}}}{2}=\frac{9,5m\pm 0.5m}{2}$ , also $x_{1}=5m,\: x_{2}=4,5m$ und für $y_{1}=4,5m,\: y_{2}=5m$ .

An diese Fülle von Aufgaben schließt sich eine weitere Lösungsmethode an: der Satz von Vieta

Satz von Vieta

Jede quadratische Gleichung $ax^{2}+bx+c=0$ lässt sich durch Division durch $a\neq 0$ auf die sogenannte Normalform $x^{2}+\frac{b}{a}x+\frac{c}{a}=0$ bringen, mit $p:=\frac{b}{a},\: q:=\frac{c}{a}$ folgt $x^{2}+pq+q=0$ .

Damit lautet der Satz von Vieta: Zwischen den Lösungen $x_{1},\: x_{2}$ und den Koeffizienten der quadratischen Gleichung in Normalform $x^{2}+px+q=0$ besteht folgender Zusammenhand: $p=-\left( x_{1}+x_{2}\right)$ und $q=x_{1}x_{2}$ .

Beispiel: $x^{2}+11x+18=0$
Um die gesuchten Lösungen zu finden, müssen die Teiler von 18 betrachtet werden: 1, 2, 3, 6, 9, 18. Für $q=18$ ergeben sich geeignete Zerlegungen: $18=1\cdot 18=2\cdot 9=3\cdot 6=\left( -1\right) \cdot \left( -18\right) =\ldots$ . Wegen $-p=x_{1}+x_{2}$ gilt hier: $x_{1}=-2,\: x_{2}=-9$ . An verschieden Übungsaufgaben schließen sich Textaufgaben an, die auf eine Zerlegung in Linearfaktoren führen. Zum Abschluss des Kapitels werden Bruchgleichungen von der Form $\frac{x^{2}}{x^{2}-x-6}+\frac{1}{x-3}=\frac{x}{2\left( x+2\right) }$ gelöst.

(x - 5) • (x + 2) = 0

x2 + 2x - 5x -10 = 0

x2 - 3x -10 = 0

Du siehst hoffentlich sofort, dass diese Gleichung die Lösungen x₁ = 5 und x₂ = -2 hat? Nein? Wann ist ein Produkt gleich Null? Siehste! Nachdenken hilft!

Es gilt: 5 + (-2) = 3 und 5 • (-2)= -10

(x + 7)(x - 1) = 0

x2 - 1x + 7x - 7 = 0

x2 + 6x - 7 = 0

Die Lösungen sind: x₁ = -7 und x₂ = 1

Es gilt: -7 +1 = - 6 und 7 • (-1) = -7

(x + 2)(x + 9) = 0

x2 + 9x + 2x + 18 = 0

x2 + 11x + 18 = 0

Die Lösungen sind: x₁ = - 2 und x₂ = - 9

Es gilt: - 2 + (- 9) = - 11 und (- 2) • (- 9) = 18

Erkennst Du die Gesetzmäßigkeit, die Herr Vieta entdeckt hat? Sucht man die Lösungen zur Gleichung 0 = x2 + x - 6 , so kann man versuchen, den rechten Teil der Gleichung in ein Produkt umzuformen. Dies geht oft recht gut, wenn Du z.B. die obigen Beispiele rückwärts liest. In diesem Fall kann die Zahl "-6"entstanden sein als das Produkt der Zahlen "2"und "-3"oder auch von "-2"und "3"oder ... Nun muss aber auch die Summe der beiden Werte passen: es muss die erste Zahl plus zweite Zahl den Wert vor dem "x" mit umgekehrten Vorzeichen ergeben! Hier passt die Kombination "2"und "-3".

Es gilt also:

0 = x² + x - 6 anders:
0 = (x - 2) • (x + 3) und damit:
x₁ = 2 und x₂ = -3

Wann kannst Du nun dieses "Zerlegen in Linearfaktoren", so nennt man das nämlich, zur Lösung von quadratischen Gleichungen verwenden?

Die Grundvoraussetzung ist, dass Du die Gleichung auf die Form x² +px + q = 0 gebracht hast. Dann brauchst Du etwas Intuition, Übung und Glück. Bei Gleichungen wie
x² - 2/7x + 8/15 = 0 würde ich es erst gar nicht versuchen, sondern die Lösungsformel benutzen. So jetzt darfst Du ein wenig üben und die Beispiele hier lassen sich alle mit Vieta lösen.

1x² +1x -56= 0

So und jetzt habe ich Dir hier noch einen Gleichungslöser für quadratische Gleichungen der Form x² +px + q = 0 eingebaut. Den kannst Du benutzen, wenn Du mit Vieta nicht zurecht kommst oder Deine Hausaufgaben kontrollieren willst.

Diese Seite wurde zuletzt am Mittwoch 13 November, 2002 20:09 geändert.
© 2002 Wolfgang Appell

François Viète
1540 - 1603

François Vieta, wie er sich in einer lateinischen Form seines Namens nannte, ist einer der Stammväter der modernen Buchstabenalgebra. In der algebraischen Symbolik und insbesondere beim Gebrauch der Buchstaben war er einer der weitreichsten auf diesem Gebiet. Vieta erkannte, dass das Rechnen mit Buchstaben und Operationssymbolen viel mehr Möglichkeiten bietet als das Rechnen mit Zahlen. Darüber hinaus hat Vieta auf dem Gebiet der Trigonometrie Hervorragendes geleistet.

Vieta stammte aus einer angesehenen bürgerlichen Familie aus Frankreich. Sein Grossvater und Vater waren beide Kaufleute. Vieta wurde in Fontenay-le-Comte geboren. Er besuchte eine Klosterschule, wo er eine gründliche Ausbildung, aber vor allem in Sprachkenntnisse bekam. Mit 18 Jahren begann Vieta Recht zu studieren. Nach dem Studium liess er sich in seiner Heimatstadt als Advokat nieder und genoss schon kurze Zeit später einen guten Ruf als Rechtsanwalt. 1564 trat er eine Stellung als Sekretär und Rechtsberater bei einer sehr einflussreichen und wohlhabenden Familie an.

Er unterrichtete ein Mädchen, das sich vor allem für Astronomie und Astrologie interessierte. Auf diese Weise entstand ein Werk von Vieta über die Darstellung der Planetentheroie auf der Grundlage des ptolemäischen geozentrischen Systems.

Nach einem Rechtsstreit wurde Vieta Advokat am Parlament in Paris. Dort lernte er verschiedene Mathematiker kennen. Die nächste Station seines Lebens war am Hof von Heinrich dem II, wo er als persönlicher Ratgeber des Königs arbeitete. Trotz der Fülle dieser Aufgaben gab er seine mathematischen Arbeiten nicht auf. Er gab ein Buch mit dem Titel "Einführung in die analytische Kunst" heraus.

Da es Vieta gesundheitlich immer schlechter ging, bat er den König 1602 um seine Entlas-sung, um zu genesen. Vieta erholte sich aber nicht mehr und starb am 23. Februar 1603 in Paris.

Fortsetzung am linken Rand!

Die p-q-Formel

Damit ist auch der Grundstein gelegt für die sogenannte p-q-Formel. Die p-q-Formel erlaubt es einem, die Lösung einer quadratischen Gleichung sofort anzugeben. Man kann die p-q-Formel einfach auswendig lernen und sie dann anwenden. Wenn man sich dabei nicht verrechnet, stimmt das Ergebnis. Es bleibt die Frage, warum das so ist. Die Antwort wird hier in der Herleitung der p-q-Formel gegeben.

Man betrachtet eine quadratische Gleichung wie oben und beginnt ebenso wie oben mit der quadratschen Ergänzung. Soweit waren wir eben schon, die Rechnung sah wie folgt aus:
Herleitung p-q-Formel, Teil 1
Jetzt macht man wie folgt weiter: Man addiert auf beiden Seiten der Gleichung und erhält so:
Herleitung p-q-Formel, Teil 2
Man erhält hier zwei Ausdrücke, da sowohl die negative als auch die positive Wurzel berücksichtigt werden muss. Beispielsweise ist sowohl 2 als auch -2 eine Wurzel von 4.
Zieht man jetzt noch auf beiden Seiten der Gleichungen ab, so erhält man die beiden Lösungen von x:
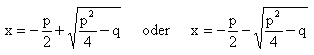
Lösungen nach der p-q-Formel
Das kann man auch so schreiben:

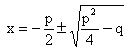
Man spricht hier von der p-q-Formel, weil man mit dieser Rechnung eine Formel für die Lösungen einer quadratischen Gleichung hat, die man ausrechnen kann, wenn man p und q aus der ursprünglichen Form der Gleichung kennt.

Hierbei gibt es noch etwas zu berücksichtigen. Die Herleitung des Ergebnisses erfolgte allgemein, also ohne besondere Bedingungen für p und q. Beim Wurzelziehen muss aber darauf geachtet werden, dass man nicht eine Wurzel aus einer negativen Zahl zieht.
Unter der Wurzel steht der Ausdruck , und dieser muss wie eben festgestellt also größer oder gleich Null sein, damit man die Wurzel überhaupt ziehen kann. Das gilt genau dann, wenn . Zusammenfassend kann man also schreiben:
Eine quadratische Gleichung der Form hat genau die beiden Lösungen
Lösungen der p-q-Formel vollständig
Gilt , so hat die quadratische Gleichung keine Lösung.

Eine quadratische Gleichung (auch Gleichung zweiter Ordnung genannt) ist eine Gleichung von der Form

a x² + b x + c = 0,

(4)

bzw. eine, die auf diese Form gebracht werden kann. Dabei sind a, b und c fixe (bekannte) Zahlen (sie heißen Koeffizienten der Gleichung) und a ¹ 0. (Wäre a = 0, wäre die Gleichung ja in Wahrheit eine lineare). Da a ¹ 0 ist, kann man beide Seiten der Gleichung durch a dividieren. Mit den Bezeichnungen b/a = p und c/a = q ergibt sich, daß eine quadratische Gleichung auch immer in der Form

x² + p x + q = 0

(5)

geschrieben werden kann. (Dies kann man auch als Normalform der quadratischen Gleichung bezeichnen. Manchmal wird sie auch p-q-Form genannt. Die Zahlen p, q heißen Koeffizienten der Gleichung in Normalform oder Parameter. Sie "numerieren" gewissermaßen die Menge aller quadratischen Gleichungen durch: Für jede konkrete Wahl dieser Zahlen ist (5) eine quadratische Gleichung). Als Grundmenge G wollen wir die Menge R der rellen Zahlen annehmen.

Die einfachsten quadratischen Gleichungen sind:

x² = 1 (sie besitzt zwei reelle Lösungen: ±1)
x² = 0 (sie besitzt eine reelle Lösung: 0)
x² = -1 (sie besitzt keine reelle Lösung)

Diese drei Beispiele charakterisieren, was auch in allgemeineren Fällen passieren kann.
(Aufgabe: Bringen Sie sie in ihre jeweilige Normalform!   Antworten:
   x² - 1 = 0, das entspricht p = 0 und q = -1,
   x² = 0, das entspricht p = 0 und q = 0,
   x² + 1 = 0, das entspricht p = 0 und q = 1.)

Kleine Lösungsformel

Für die Lösungen einer quadratischen Gleichung, die in der Normalform (5) vorliegt, gibt es eine handliche

Formel, die sogenannte (kleine) Lösungsformel. Sie lautet

x_1,2 = - p/2 ±

________
Ö p²/4 - q

(6)

Sie ist so wichtig, daß Sie wissen sollten, wo sie herkommt (der Beweis benützt die Methode des Ergänzens auf ein vollständiges Quadrat, siehe nebenstehenden Button). Außerdem sollten Sie versuchen, sie sich auswendig zu merken.

Sie hat folgende Bedeutung: Je nachdem, ob p²/4 - q (also die Zahl unter dem Wurzelzeichen) negativ, 0 oder positiv ist, gibt es keine, eine oder zwei Lösungen.

Ist p²/4 - q < 0, so steht unter dem Wurzelzeichen eine negative Zahl. Da man (im Rahmen der reellen Zahlen) die Wurzel aus einer negativen Zahl nicht ziehen kann, gibt es keine reelle Lösung. Die Lösungsmenge ist leer, L = { }.
Ist p²/4 - q = 0, so steht unter dem Wurzelzeichen 0, und da Ö0 = 0 ist, gibt es eine einzige Lösung, x = - p/2. Die Lösungsmenge ist L = {-p/2}. Die Lösungsformel gilt insofern, als sie zwei gleiche Zahlen beschreibt: x₁ = x₂ = - p/2.
Ist p²/4 - q > 0, so steht unter dem Wurzelzeichen eine positive Zahl. In diesem Fall gibt es zwei reelle Lösungen x₁ und x₂, die gerade von der Lösungsformel angezeigt werden. Die Lösungsmenge ist L = {x₁, x₂}, wobei

x₁

- p/2 -

________
Ö p²/4 - q

(7)

x₂

- p/2 +

________
Ö p²/4 - q

(8)

Die Kombination p²/4 - q entscheidet also über die Zahl der Lösungen. Sie wird Diskriminante genannt.

Im Applet
Quadratische
Gleichungen 1
können Sie den
Beweis der
Lösungsformel noch
einmal als Puzzle
durchspielen.

Im Applet
Quadratische
Gleichungen 2
werden drei
Lösungsmethoden
einander
gegenübergestellt.

Halten wir fest: Eine quadratische Gleichung hat entweder zwei, eine oder keine Lösung. Wir werden uns später von einem anderen Blickwinkel mit quadratischen Ausdrücken beschäftigen und einen geometrischen Grund dafür kennenlernen.

geometrischer
Grund

Beachten Sie beim Rechnen, daß die Wurzel aus einer reellen (nicht-negativen) Zahl per Definition immer ³ 0 ist. (So hat etwa Ö4 nur einen Wert, nämlich 2, während ± Ö4 für ± 2 steht, d.h. für die zwei Werte - 2 und 2).

Beispiel:
Gegebene Gleichung: x² - 5 x + 6 = 0 (das entspricht p = - 5 und q = 6)
Die Lösungsformel ergibt

x_1,2 = 5/2 ±

_______
Ö25/4 - 6

= 5/2 ±

___
Ö1/4

(9)

Da unter dem Wurzelzeichen eine positive Zahl auftritt (nämlich 1/4), gibt es zwei reelle Lösungen, und es darf weitergerechnet werden. Die Wurzel aus 1/4 ist gleich 1/2, und daher ergibt sich x_1,2 = 5/2 ±1/2, also x₁ = 5/2 - 1/2 = 2 und x₂ = 5/2 + 1/2 = 3. Die Lösungsmenge ist L = {2, 3}.

Wurzel
immer ³ 0

Beispiel:
Gegebene Gleichung: x² - 2 = 0 (das entspricht p = 0 und q = - 2)
Sie kann als x² = 2 geschrieben werden, woraus sich die Lösungen ±Ö2 ergeben. Die Lösungsformel ist hier also gar nicht notwendig. Wird sie dennoch benützt, so ergibt sich

x_1,2 = 0 ±

____
Ö0 + 2

= ±Ö2

(10)

Die Lösungsmenge ist L = {-Ö2, Ö2}.

Dieses Beispiel illustriert eine Tatsache, die auch aus der Lösungsformel (6) ersichtlich ist: Für ganzzahlige Koeffizienten p, q enthalten die Lösungen Wurzeln aus rationalen Zahlen (d.h. aus Brüchen, die in Spezialfällen ganze Zahlen sein können). Sie sind daher im Allgemeinen irrational. Nur in Einzelfällen (die allerdings häufig als Beispiele ausgewählt werden) sind die auftretenden Wurzeln selbst wieder rational (oder sogar ganzzahlig).

rationale und
irrationale Zahlen

Der Vietasche Satz

Unkonventionelle Fragestellung: Geben Sie eine quadratische Gleichung an, die die Lösungen 1 und 2 hat!
Antwort: Versuchen Sie's mit der Gleichung

( x - 1) ( x - 2 ) = 0 .

(11)

Ohne jede Rechnung ist ersichtlich, daß sie für x = 1 eine wahre Aussage ist (denn dann ist ja der erste der beiden Faktoren Null), und daß sie für x = 2 eine wahre Aussage ist (denn dann ist der zweite der beiden Faktoren Null).

Um diesen einfachen Lösungsweg zu verschleiern, multiplizieren wir die Klammer aus und finden

( x - 1 ) ( x - 2 ) = x² - 3 x + 2.

(12)

Beachten Sie, daß das keine Gleichung ist, sondern eine Identität. Wir haben hier einfach zwei Möglichkeiten, ein und dieselbe Sache darzustellen. Dies können wir benützen, um die Gleichung (11) in der Form

x² - 3 x + 2 = 0

(13)

anzuschreiben. Die linke Seite ist nach wie vor das Produkt aus x - 1 und x - 2, nur sieht man das jetzt nicht mehr so schnell. Folglich sind die Lösungen die Zahlen 1 und 2. Mit dieser Methode zaubern LehrerInnen quadratische Gleichungen hervor, deren Lösungen sie im Voraus kennen!

Identitäten

Hinter diesem Vorgang verbergen sich tiefere Zusammenhänge, die erst nach und nach beim Fortschreiten des Stoffs klarer werden.

Um einen kleinen Vorgeschmack davon zu bekommen, wiederholen wir das Argument, legen uns aber jetzt auf die Werte der Lösungen nicht fest, sondern bezeichnen sie lediglich mit x₁ und x₂. Die quadratische Gleichung, die x₁ und x₂ als Lösungen hat, lautet

( x - x₁ ) ( x - x₂ ) = 0 .

(14)

Wieder multiplizieren wir den Term auf der linken Seite aus und erhalten

( x - x₁ ) ( x - x₂ ) = x² - ( x₁ + x₂ ) x + x₁ x₂ ,

(15)

und wieder ist das eine Identität: zwei Möglichkeiten, ein und dieselbe Sache darzustellen. Daher kann die Gleichung (14) auch in der Form

x² - ( x₁ + x₂ ) x + x₁ x₂ = 0

(16)

angeschrieben werden, und wieder wissen wir ohne weitere Rechnung, daß sie die Lösungen x₁ und x₂ besitzt. Diese Gleichung ist aber nichts anderes als die Normalform (5), d.h. sie ist von der Form x² + p x + q = 0 , wobei

- (x₁ + x₂ )

(17)

x₁ x₂ .

(18)

Man kann die Lösungen, die herauskommen sollen, also vorgeben und sich mit Hilfe dieser Formeln die Gleichung ausrechnen!

Diese Aussage heißt Satz von Vieta (auch Vietascher Wurzelsatz genannt). Sie wird üblicherweise in der Form

x₁ + x₂

- p

(19)

x₁ x₂

(20)

angeschrieben. In Worten ausgedrückt lautet sie: Falls die quadratische Gleichung x² + p x + q = 0 zwei reelle Lösungen x₁ und x₂ hat, so ist die Summe der beiden Lösungen - p, und ihr Produkt ist q. Der Satz gilt auch, wenn die Gleichung nur eine Lösung (nämlich -p/2) hat und x₁ = x₂ ( = -p/2) gesetzt wird.

quadratische
Funktionen

Man kann den Vietaschen Satz übrigens auch durch direkte Rechnung beweisen, indem die Lösungsformeln für x₁ und x₂ verwendet werden.

Beispiel: Die Gleichung x² - 5 x + 6 = 0 , die oben bereits betrachtet und gelöst wurde, hat die Lösungen 2 und 3. Deren Summe ist 5 (also gerade das Negative von p = -5) und ihr Produkt ist 6 (also gerade q).

Eine der hinter dem Vietaschen Satz liegenden Einsichten ist die Tatsache, daß jeder Term der Form x² + p x + q, sofern er für zumindest eine reelle Zahl x Null ist, als Produkt von Linearfaktoren geschrieben werden kann. (Ein linearer - genauer: linear-inhomogener - Term ist ein Ausdruck der Form a x + b. Er heißt auch Polynom erster Ordnung. Ein Term der Form x² + p x + q oder, ein bißchen allgemeiner, a x² + b x + c, heißt quadratischer Term oder Polynom zweiter Ordnung).

Polynome

Aufgabe: Schreiben Sie den Term x² - 5 x + 6 als ein Produkt von Linearfaktoren!
Antwort: Die Lösungen der zugehörigen quadratischen Gleichung sind, wie schon oben berechnet, 2 und 3. Daher gilt die Identität x² - 5 x + 6 = ( x - 2 ) ( x - 3 ), was durch Ausmultiplizieren der Klammern überprüft werden kann.

Die Beschäftigung mit Gleichungen hat uns also zu einer Methode geführt, wie manche quadratische Ausdrücke in elementarere Bestandteile ''zerlegt'' werden können. Die beiden Linearfaktoren sind so etwas Ähnliches wie die Primfaktoren einer natürlichen Zahl: Die Zahl 35 läßt sich als 5×7 schreiben, wobei 5 und 7 auch als ''Bestandteile'' gedeutet werden können.

Primfaktoren

Große Lösungsformel

Eine quadratische Gleichung kann auch in der Form (4), also

a x² + b x + c = 0,

(21)

gegeben sein. Dabei muß, wie bereits festgestellt, a ¹ 0 sein, und der Zusammenhang zur Normalform ist durch p = b/a und q = c/a gegeben (was sich nach Division beider Seiten durch a ergibt). Dann lautet die entsprechende (große) Lösungsformel

x_1,2 =

- b ±

________
Ö b² - 4 a c

2 a

(22)

Je nachdem, ob die unter dem Wurzelzeichen stehende Zahl b² - 4 a c negativ, 0 oder positiv ist, hat die Gleichung keine, eine oder zwei reelle Lösungen. Die große ergibt sich aus der kleinen Lösungsformel, indem einfach p = b/a und q = c/a eingesetzt wird.

Die Kombination b² - 4 a c entscheidet also über die Zahl der Lösungen. Sie übernimmt die Rolle, die bei der kleinen Lösungsformel die Kombination p²/4 - q gespielt hat und wird, wie diese, Diskriminante genannt.

Beweis:
Seien a und b zwei Zahlen so, dass a + b = -p und ab=q.
a + b = -p ist gleichbedeutend mit -(a + b) = p, wie man sieht, wenn man die Gleichung mit -1 multipliziert.
Also kann man in der Gleichung p durch -(a + b) ersetzen, und q durch ab. Dann ergibt sich:

Beweis Satz von Vieta
Also sind a und b Lösungen der Gleichung.
q.e.d.

Der Satz von Vieta kann also dann hilfreich sein, wenn man ihn gut einübt. Es geht dabei darum, die beiden Zahlen a und b zu "erraten", und das lässt sich einigermaßen trainieren.